Week 2: Differentiability

Demo by Christian Mikkelstrup, Hans Henrik Hermansen, Karl Johan Måstrup Kristensen and Magnus Troen

from sympy import *
from dtumathtools import *
init_printing()

When it comes to Python/CAS and differentiability, we face the same difficulties as with continuity. Python/CAS is not very suitable for proving differentiability. It can, however, be a powerful tool once differentiability is proven/assumed. In this demo we will show how CAS/python can be used when working with differentiable functions.

Vector Functions

Vector functions of multiple variables are defined by def 1.3.1 and can be writen as

\[\begin{split}\boldsymbol{f}(\boldsymbol{x}) = \begin{bmatrix} f_1(\boldsymbol{x}) \\ \vdots \\ f_k(\boldsymbol{x}) \end{bmatrix}\end{split}\]

We already know examples of vector functions of several variables from linear algebra, namely linear mappings from \(\mathbb R^n\) to \(\mathbb R^k\). Which for an arbitrary \(k \times n\) matrix \(A\) and a vector \(\boldsymbol{x} \in \mathbb R^n\) will have the form

\[\begin{split}\boldsymbol{f}(\boldsymbol{x}) = A\boldsymbol{x} = \begin{bmatrix} f_1(\boldsymbol{x}) \\ \vdots \\ f_k(\boldsymbol{x}) \end{bmatrix}.\end{split}\]

Here, the functions \(f_1, f_2, \ldots, f_k\) are determined by the matrix-vector multiplication you know from Mat1a.

We now extend the concept to general vector functions of several variables, where the coordinate functions \(f_1, f_2, \ldots, f_k\) are not limited by the rules of matrix-vector multiplication, \(f_i(x_1,x_2,x_3) = c_1x_1 + c_2x_2 + c_3x_3\) . A coordinate function \(f_i\) could, for example, have the formula \(f_i(x_1,x_2,x_3) = x_1 \sin(x_2) + x_3^2\).

I SymPy vector functions can be constructed using Matrix-objects or callable functions:

# Example of a vector function using the Matrix class
x1, x2, x3 = symbols('x1:4')

f_expr = Matrix([
    x1 * sin(x2) + x3**2,
    x1*x2*x3,
    x1**2 + 4*x2 * x3
])
f_expr

\[\begin{split}\displaystyle \left[\begin{matrix}x_{1} \sin{\left(x_{2} \right)} + x_{3}^{2}\\x_{1} x_{2} x_{3}\\x_{1}^{2} + 4 x_{2} x_{3}\end{matrix}\right]\end{split}\]

Which can be evaluated with \(\verb|.subs()|\)

f_expr.subs({x1: 1, x2: 2, x3: 3})

\[\begin{split}\displaystyle \left[\begin{matrix}\sin{\left(2 \right)} + 9\\6\\25\end{matrix}\right]\end{split}\]

If you prefere functions, the same can be achieved with

def f(x1, x2, x3):
    return Matrix([
        x1 * sin(x2) + x3**2,
        x1*x2*x3,
        x1**2 + 4 * x2 * x3
    ])

f(x1,x2,x3)

\[\begin{split}\displaystyle \left[\begin{matrix}x_{1} \sin{\left(x_{2} \right)} + x_{3}^{2}\\x_{1} x_{2} x_{3}\\x_{1}^{2} + 4 x_{2} x_{3}\end{matrix}\right]\end{split}\]

f(1,2,3)

\[\begin{split}\displaystyle \left[\begin{matrix}\sin{\left(2 \right)} + 9\\6\\25\end{matrix}\right]\end{split}\]

Both approches yields the same results. Which method you chose is up to personal preference.

Gradient Vector

An example of a vector function is the gradient vector, as introduced last week:

\[\nabla f(\boldsymbol{x}):=\left(\frac{\partial f}{\partial x_1}(\boldsymbol{x}),\frac{\partial f}{\partial x_2}(\boldsymbol{x}),\ldots, \frac{\partial f}{\partial x_n}(\boldsymbol{x})\right).\]

This can be considered as the map \(\nabla f: \mathbb R^n \to \mathbb R^n\).

As an example we will consider the gradient of the function \(f: \mathbb{R}^2 \to \mathbb{R}\), defined by \(f(\boldsymbol{x}) = 1 - \frac{x_1^2}{2} -\frac{x_2^2}{2}\)

x1, x2 = symbols('x1:3')
f = 1 - x1**2 / 2 - x2**2 / 2

Nabla = dtutools.gradient(f)

f, Nabla

\[\begin{split}\displaystyle \left( - \frac{x_{1}^{2}}{2} - \frac{x_{2}^{2}}{2} + 1, \ \left[\begin{matrix}- x_{1}\\- x_{2}\end{matrix}\right]\right)\end{split}\]

This gives us a vector function \(\nabla f: \mathbb R^2 \to \mathbb R^2\) defined by \(\nabla f(x_1, x_2) = (-x_1, -x_2)\). Which for example can be evaluated in \(\boldsymbol{x}_0 = (1, -1)\) which yields:

Nabla.subs({x1: 1, x2: -1})

\[\begin{split}\displaystyle \left[\begin{matrix}-1\\1\end{matrix}\right]\end{split}\]

Directional Derivatives

Consider the same function \(f: \mathbb{R}^2 \to \mathbb{R}\), med forskriften \(f(\boldsymbol{x}) = 1 - \frac{x_1^2}{2} -\frac{x_2^2}{2}\)

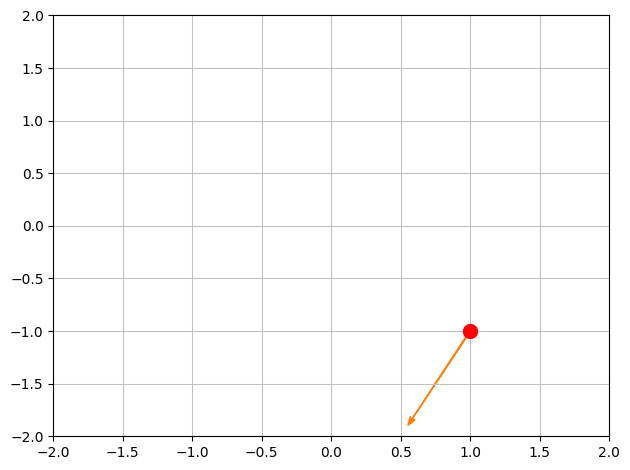
We wish to find the directional derivative of \(f\) in the point \(\boldsymbol{x_0} = (1,-1)\) in the direction of the unit vector \(\boldsymbol{e}\)

x0 = Matrix([1,-1])
e = Matrix([-1,-2]).normalized()
e, N(e)

\[\begin{split}\displaystyle \left( \left[\begin{matrix}- \frac{\sqrt{5}}{5}\\- \frac{2 \sqrt{5}}{5}\end{matrix}\right], \ \left[\begin{matrix}-0.447213595499958\\-0.894427190999916\end{matrix}\right]\right)\end{split}\]

p1 = dtuplot.scatter(x0, rendering_kw={"markersize":10,"color":'r'}, xlim=[-2,2],ylim=[-2,2],show=False)
p1.extend(dtuplot.quiver(x0,e,show=False))
p1.show()

We compute the gradient in \(\boldsymbol{x_0}\):

Nabla = Matrix([diff(f,x1),diff(f,x2)]).subs({x1:x0[0],x2:x0[1]})
Nabla

\[\begin{split}\displaystyle \left[\begin{matrix}-1\\1\end{matrix}\right]\end{split}\]

Now the directional derivative is given by \(\nabla_{\boldsymbol{e}} f(\boldsymbol{x_0}) = \braket{\boldsymbol{e},f(\boldsymbol{x_0})}\).

a = e.dot(Nabla)
a

The Hessian Matrix

When we have to use a concept of the curvature of multivariate scalar functions (relevant later for extrema analysis and Taylor expansion), we have to start with second-order partial derivatives. The information about these second-order derivatives is collected in the Hessian matrix described in definition 3.5.1.

It can be constructed manually in SymPy from a given function with its associated second-order partial derivative.

f = 1-x1**2/2-x2**3/2*x3 + x1*x3
f

fx1x1 = f.diff(x1,2)
fx1x2 = f.diff(x1,x2)
fx1x3 = f.diff(x1,x3)
fx2x2 = f.diff(x2,2)
fx2x3 = f.diff(x2,x3)
fx3x3 = f.diff(x3,2)

H1 = Matrix([
    [fx1x1, fx1x2, fx1x3],
    [fx1x2, fx2x2, fx2x3],
    [fx1x3, fx2x3, fx3x3]
])

H1

\[\begin{split}\displaystyle \left[\begin{matrix}-1 & 0 & 1\\0 & - 3 x_{2} x_{3} & - \frac{3 x_{2}^{2}}{2}\\1 & - \frac{3 x_{2}^{2}}{2} & 0\end{matrix}\right]\end{split}\]

Which ofcourse has an equivalent function implemented in \(\verb|dtumathtools|\)

H2 = dtutools.hessian(f)
H2

\[\begin{split}\displaystyle \left[\begin{matrix}-1 & 0 & 1\\0 & - 3 x_{2} x_{3} & - \frac{3 x_{2}^{2}}{2}\\1 & - \frac{3 x_{2}^{2}}{2} & 0\end{matrix}\right]\end{split}\]

Which in both cases can be evaluated with \(\verb|.subs()|\)

H1.subs({x1:1,x2:2,x3:3}), H2.subs({x1:1,x2:2,x3:3})

\[\begin{split}\displaystyle \left( \left[\begin{matrix}-1 & 0 & 1\\0 & -18 & -6\\1 & -6 & 0\end{matrix}\right], \ \left[\begin{matrix}-1 & 0 & 1\\0 & -18 & -6\\1 & -6 & 0\end{matrix}\right]\right)\end{split}\]

The Jacobian Matrix

Definition 3.8.1 allows us to also differentiate multivariate vector functions in the form of the Jacobian matrix. To illustrate this, we define the function \(\boldsymbol{f}: \mathbb{R}^4 \to \mathbb{R}^3\):

\[\begin{split} \boldsymbol{f} (\boldsymbol{x}) = \begin{bmatrix} f_1(\boldsymbol{x})\\ f_2(\boldsymbol{x})\\ f_3(\boldsymbol{x}) \end{bmatrix} = \left[\begin{matrix}x_{1}^{2} + x_{2}^{2} x_{3}^{2} + x_{4}^{2} - 1\\x_{1} + \frac{x_{2}^{2}}{2} - x_{3} x_{4}\\x_{1} x_{3} + x_{2} x_{4}\end{matrix}\right] \end{split}\]

x1,x2,x3,x4 = symbols('x1:5', real = True)

f = Matrix([
    x1**2 + x2**2 * x3**2 + x4**2 - 1,
    x1 + x2**2/2 - x3 * x4,
    x1 * x3 + x2 * x4
])

f

\[\begin{split}\displaystyle \left[\begin{matrix}x_{1}^{2} + x_{2}^{2} x_{3}^{2} + x_{4}^{2} - 1\\x_{1} + \frac{x_{2}^{2}}{2} - x_{3} x_{4}\\x_{1} x_{3} + x_{2} x_{4}\end{matrix}\right]\end{split}\]

Note that \(f_1, f_2, f_3\) are differentiable for all \(\boldsymbol{x} \in \mathbb R^4\), and we can compute the Jacobian matrix as $\( \boldsymbol{J_f} = \begin{bmatrix} \nabla f_1^T\\ \nabla f_2^T \\ \nabla f_3^T\end{bmatrix} \)$

This can be done manually:

J_f = Matrix.vstack(dtutools.gradient(f[0]).T, dtutools.gradient(f[1]).T, dtutools.gradient(f[2]).T)
J_f

\[\begin{split}\displaystyle \left[\begin{matrix}2 x_{1} & 2 x_{2} x_{3}^{2} & 2 x_{2}^{2} x_{3} & 2 x_{4}\\1 & x_{2} & - x_{4} & - x_{3}\\x_{3} & x_{4} & x_{1} & x_{2}\end{matrix}\right]\end{split}\]

It can also be done using SymPy’s command \(\verb|jacobian|\):

J = f.jacobian([x1,x2,x3,x4])
J

\[\begin{split}\displaystyle \left[\begin{matrix}2 x_{1} & 2 x_{2} x_{3}^{2} & 2 x_{2}^{2} x_{3} & 2 x_{4}\\1 & x_{2} & - x_{4} & - x_{3}\\x_{3} & x_{4} & x_{1} & x_{2}\end{matrix}\right]\end{split}\]

Parametric Curves in the (x,y) Plane and their Tangents

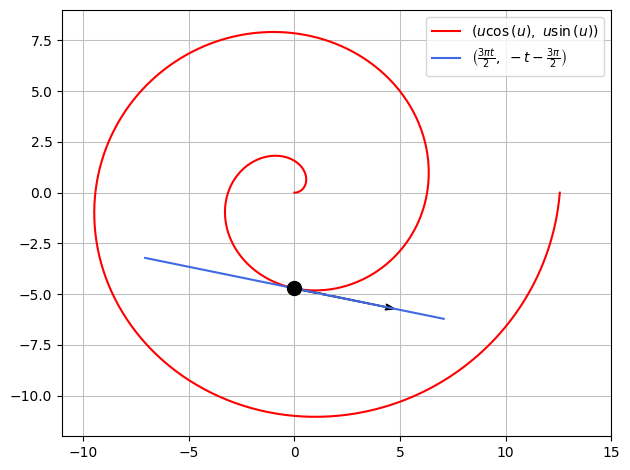
Consider the spiral with the given parametric representation,

u, t = symbols('u t', real=True)
r = Matrix([u*cos(u), u*sin(u)])
r

\[\begin{split}\displaystyle \left[\begin{matrix}u \cos{\left(u \right)}\\u \sin{\left(u \right)}\end{matrix}\right]\end{split}\]

The tangent vector in a given point is given by

rd = diff(r,u)
rd

\[\begin{split}\displaystyle \left[\begin{matrix}- u \sin{\left(u \right)} + \cos{\left(u \right)}\\u \cos{\left(u \right)} + \sin{\left(u \right)}\end{matrix}\right]\end{split}\]

We will now find the parametric representation of the tangent of the spiral at \(((0,-\frac{3\pi}{2}))\), corresponding to the parametric value \(u_0 = \frac{3\pi}{2}\), which is seen by

u0 = 3*pi/2
rdu0 = rd.subs(u,u0)
ru0 = r.subs(u,u0)
ru0

\[\begin{split}\displaystyle \left[\begin{matrix}0\\- \frac{3 \pi}{2}\end{matrix}\right]\end{split}\]

The parametric representation for the tangent in \(u_0\) is found by

T = ru0 + t*rdu0
T

\[\begin{split}\displaystyle \left[\begin{matrix}\frac{3 \pi t}{2}\\- t - \frac{3 \pi}{2}\end{matrix}\right]\end{split}\]

Which we can now visualize as

p = dtuplot.plot_parametric(r[0], r[1],(u,0,4*pi),rendering_kw={"color":"red"},use_cm=False,show=False)
p.extend(dtuplot.plot_parametric(T[0],T[1],(t,-1.5,1.5),rendering_kw={"color":"royalblue"},use_cm=False,show=False))
p.extend(dtuplot.scatter(ru0,rendering_kw={"markersize":10,"color":'black'}, show=False))
p.extend(dtuplot.quiver(ru0,rdu0,rendering_kw={"color":"black"},show=False))
p.xlim = [-11,15]
p.ylim = [-12,9]

p.show()