Week 1: Continuity, Plotting, and Partial Derivatives

Demo by Christian Mikkelstrup, Hans Henrik Hermansen, Jakob Lemvig, Karl Johan Måstrup Kristensen og Magnus Troen

from sympy import *
from dtumathtools import *
init_printing()

Welcome back after Christmas and January, and welcome to spring in mat1. There will be a whole lot of new curriculum, and among other things a whole lot of 3D plots! For this we have developed dtumathtools, which will accompany you during the spring. It contains dtuplot which should be used for plotting, as well as several good helper functions. You should have dtumathtools installed from mat1a, if not, please run the command

pip install -U dtumathtools 

in your terminal.

Functions (of One Variable)

We can define the function \(f: \mathbb{R} \to \mathbb{R}\), \(f(x)=x \mathrm{e}^x\) as a python function using the familiar command:

def f(x):  
    return x * exp(x)

The function is evaluated in the point \(x = -2\) with the command:

f(-2)

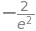
Which has the nummerical value:

f(-2).evalf()

It is, however, rarely necessary to define functions with the def-command, and we wil often work directly with the function expression:

x = symbols('x', real = True)          # necessary to use x as a symbolic variable (note the real=True, since R -> R)
f_expr = x * exp(x)
f_expr

Which is evaluated by:

f_expr.subs(x, -2)

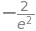
The function can be differentiated by:

f_maerke = f_expr.diff(x)
f_maerke

We can also investigate the limits for \(x \to -\infty\), \(x \to \infty\) and \(x \to -2\) with the commands:

f_expr.limit(x, -oo), f_expr.limit(x, oo), f_expr.limit(x, -2)

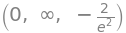
It should be no surprise that \(\lim_{x \to -2} f(x) = f(-2)\), since the function is continuous everywhere.

We can plot the function and its derivative by:

plot(f_expr, f_maerke, (x, -5, 1))

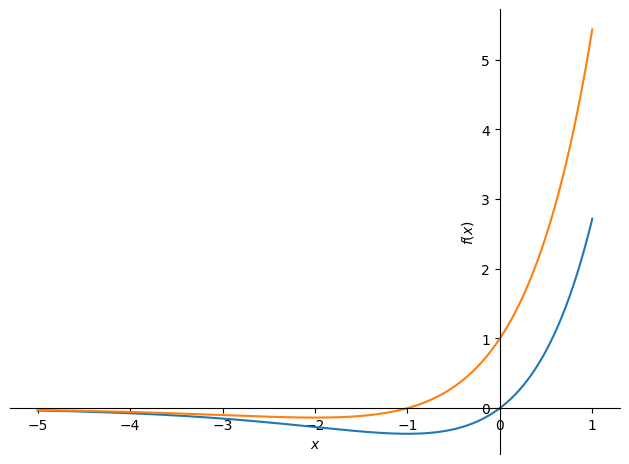
<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x7f7dcaf240a0>

A little more complicated example could be the piecewise defined function \(g: \mathbb{R} \to \mathbb{R}\):

\[\begin{equation*} g(x) = \begin{cases} -x & x <0 \\ \mathrm{e}^x & x \ge 0 \end{cases} \end{equation*}\]

Which in pyhton would be defined by:

def g(x):
    if x < 0:
        return -x
    else:
        return exp(x)

Which again is preferable to define using Sympy:

g_expr = Piecewise((-x, x < 0), (exp(x), x >= 0))
g_expr

\[\begin{split}\displaystyle \begin{cases} - x & \text{for}\: x < 0 \\e^{x} & \text{otherwise} \end{cases}\end{split}\]

Which is evaluated as expected:

g_expr.subs(x, -2)

And plotted using:

plot(g_expr,(x,-5,2), ylabel='g(x)')

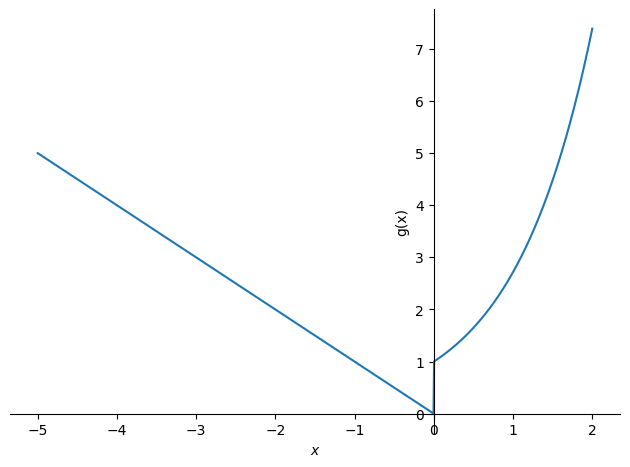
<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x7f7dc8c92a30>

Notice the function is discontinuous in \(x = 0\). Note that Python/CAS cannot be used to prove discontinuity in \(x = 0\). This would require a so called epsilon-delta-argument, which Python/CAS cannot help us with. Sympy will, for example, differentiate the function without raising any suspicion of discontinuity.

g_expr.diff(x)

\[\begin{split}\displaystyle \begin{cases} -1 & \text{for}\: x < 0 \\e^{x} & \text{otherwise} \end{cases}\end{split}\]

We should, however, note that the function isn’t differentiable in \(x = 0\), since it isn’t continuous in this point.

Partial Derivatives using diff

For functions of multiple variables we will introdue the partial derivative, aswell as how they can be used. To showcase the partial derivatives we will consider the function:

x, y = symbols('x y')
f = x*y**2+x
f

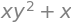
which can be differentiated using diff

f.diff(x), f.diff(y)

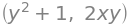
Each of these expression can be differentiated w.r.t \(x\) and \(y\). Which yields these four functions.

f.diff(x).diff(x), f.diff(x).diff(y), f.diff(y).diff(x), f.diff(y).diff(y)

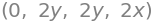
These are called the second order derivatives and can be computed directly by:

f.diff(x,2), f.diff(y,2), f.diff(x,y), f.diff(y,x)

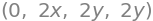
As last semester we can input values for x and y. For example \(\frac{\partial}{\partial x}f(x,y)\) evaluated in \((-2,3)\)

f.diff(x).subs({x:-2,y:3})

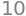
or \(\frac{\partial}{\partial x\partial y}f(x,y)\), evaluated in \((5,-13)\)

f.diff(x,y).subs({x:5,y:-13})

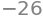
Plots

Orienting Graphs

We will now consider functions of multiple variables, hence plotting in 3D! This leaves us a decission to make, since we need to chose which angle we want to see the graphs from. If we don’t do anything dtuplot, will chose an angle for us, but if we wish to inspect the graph from a certain angle, then camera can be used. Try changing the values for elev and azim.

f = 4-x**2-y**2

p=dtuplot.plot3d(f, (x,-3,3),(y,-3,3), camera = {"elev": 25, "azim": 45})

The plot above was generated as a static PNG-file, which is greate if you wish to print or export the Notebook as a PDF. All plots will be static if we don’t do anything or if we use the command %matplotlib inline.

If we intead run the command %matplotlib qt (which in the following block has been commented out, try running the block after removing #), then we enable interactive plots. All subsequent plots, will now “pop out” of VS Code, where we now can rotate the graph.

#%matplotlib qt

About Interactive Plots

Note: %matplotlib qt only works when running python on your own computer. It will, for instance, not work if you run Python on an online server like Google Colab. In such cases, widgets can be used instead %matplotlib ipympl. This does, however, require you to intall the package ipympl.

Overview of commands:

# %matplotlib inline        # static plots
# %matplotlib qt            # QT (cute) interactive pop-out plots
# %matplotlib ipympl        # Widget/ipynpl interactive inline plots (not as stable as QT, may require a restart of the kernel)
# %matplotlib --list        # list of all backends

Aesthetics

When we wish to change the aesthetics of our plots, we’ll need to use redering_kw={...} which may look intimidating. It just tells which rendering settings to use, for example color, alpha etc. In most cases it’s adequate to just write {...}, which dtuplot will know means aesthetics.

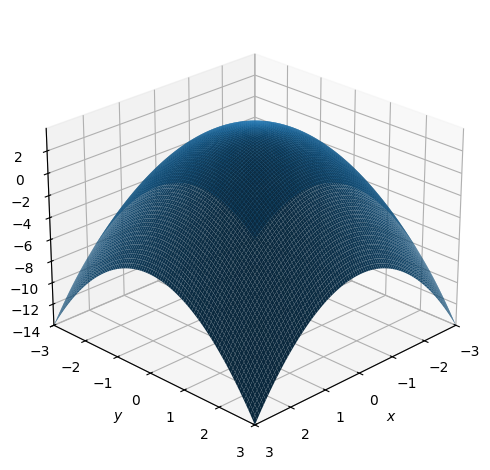
dtuplot.plot3d(f, (x,-3,3),(y,-3,3), wireframe = True, rendering_kw = {"color": "red", "alpha": 0.5})

<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f7dc8c2ae80>

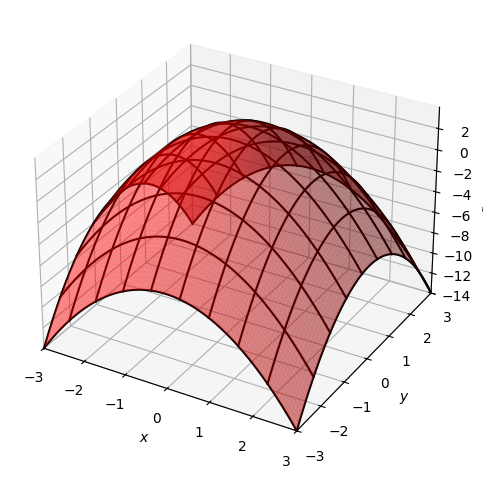
Some aesthetic choices are special enough to be outside of redering_kw, for example wireframe as seen above, or use_cm which denotes each value with a color, as seen below.

p=dtuplot.plot3d(f, (x,-3,3),(y,-3,3), use_cm=True, legend=True)

Contours

We can also plot contours, i.e. a 2D plot of a 3D structure by:

dtuplot.plot_contour(f, (x,-3,3),(y,-3,3), is_filled=False)

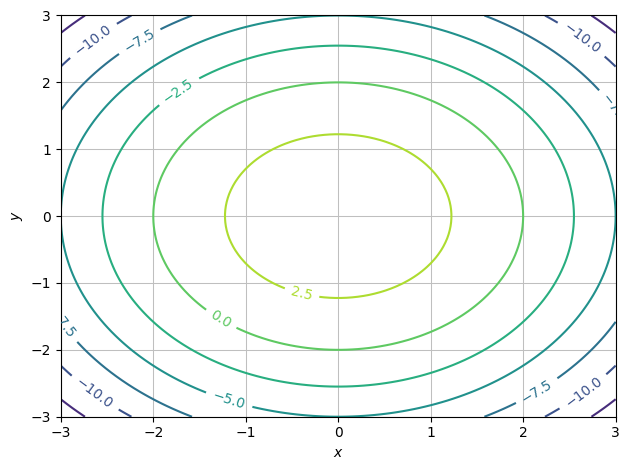
<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f7dc8bd1730>

And if we wish to chose the exact values shown:

zvals = [-2,-1,0,1]
dtuplot.plot_contour(f, (x,-3,3),(y,-3,3), rendering_kw={"levels":zvals, "alpha":0.5}, is_filled=False)

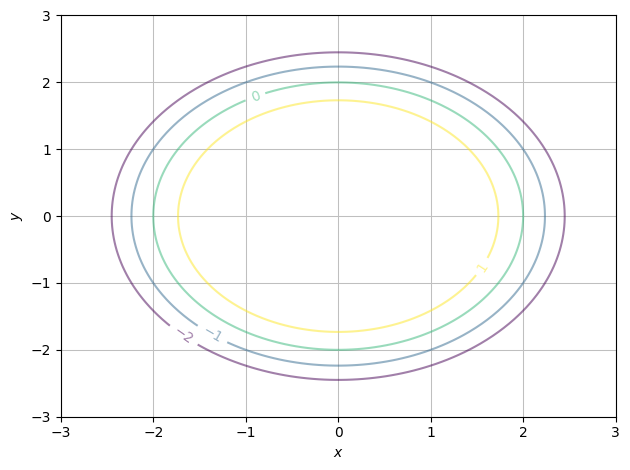
<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f7dc7f6dc40>

Gradient Vector Fields

Consider the vector field

(5)\[\begin{equation} f(x,y)=\cos(x)+\sin(y). \end{equation}\]

The gradient of \(f\) can be computed as:

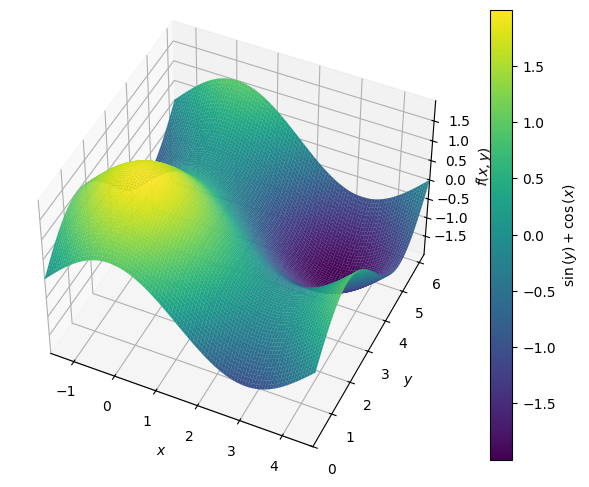
f = cos(x)+sin(y)
nf = Matrix([f.diff(x), f.diff(y)])
nf

\[\begin{split}\displaystyle \left[\begin{matrix}- \sin{\left(x \right)}\\\cos{\left(y \right)}\end{matrix}\right]\end{split}\]

The gradient can also be computed using dtutools.gradient. Note that this function doesn’t tell us in which order the variables are differentiated.

dtutools.gradient(f)

\[\begin{split}\displaystyle \left[\begin{matrix}- \sin{\left(x \right)}\\\cos{\left(y \right)}\end{matrix}\right]\end{split}\]

The gradient vector field can be plotted as shown:

dtuplot.plot_vector(nf, (x,-pi/2,3/2*pi),(y,0,2*pi),scalar=False)

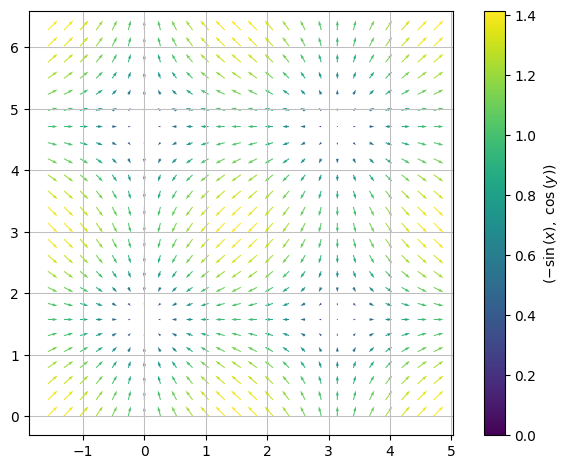
<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f7dc86c3f70>

Or if we want to get fancy (note that rendering_kw has been split, such that the arrows and contours have their own list of aethetics).

dtuplot.plot_vector(nf, (x,-pi/2,3/2*pi),(y,0,2*pi),
    quiver_kw={"color":"black"},
    contour_kw={"cmap": "Blues_r", "levels": 20},
    grid=False, xlabel="x", ylabel="y",n=15)

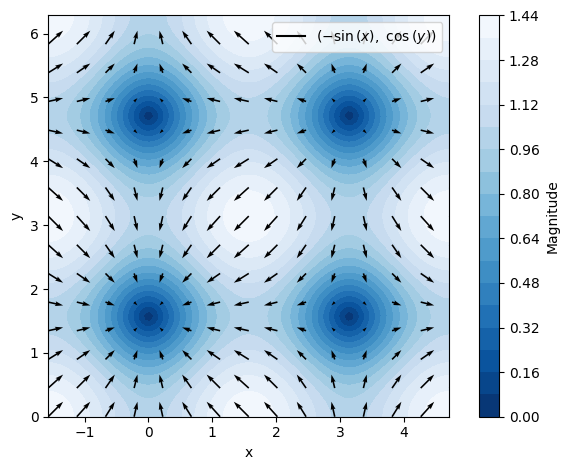
<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f7dc8b6f3d0>

Which in 3D can be visualised as

p = dtuplot.plot3d(f, (x,-pi/2,3/2*pi),(y,0,2*pi),use_cm=True, camera={"elev":45, "azim":-65}, legend=True)