Week 1: Preparation#
Reading Material#
We recommend that you read the textbook. Watching YouTube videos on the week’s topics can be useful, but it should not replace proper preparation for the week’s program and is not recommended as a standalone approach.
Read and study the following:
Review: Study Chapter 0
Long Day: Chapter 1, Section 2.1, Section 3.1 and Section 3.2
Short Day: Sections 2.2, 3.2 and 3.3
Python demo01
Key Concepts#
After reading, you should be able to explain the following key concepts:
Scalar functions: particularly quadratic forms
Vector functions
Visualization of functions: Graphs and level curves/sets
Continuity
The standard inner product (dot product) and norm in \(\mathbb{R}^n\)
Partial derivatives and the Gradient vector
This week, we will explore these key concepts in great detail. We expect you to have familiarized yourself with these topics before lectures.
Preparatory Exercises#
I: The Function Value at a Point#
Question a#
Substitute the values \(x = 2\) and \(y = -1\) into the functional expression \(f(x, y) = x^2 + 3xy + 4y^2\) and calculate \(f(2, -1)\).
Hint
Substitute \(x\) with \(2\) and \(y\) with \(-1\) in the expression \(x^2 + 3xy + 4y^2\).
Answer
\(f(2, -1) = 2^2 + 3(2)(-1) + 4(-1)^2 = 4 - 6 + 4 = 2\)
Question b#
Let \(g: \mathbb{R}^2 \to \mathbb{R}\) be given by the functional expression \(g(x_1, x_2) = x_1^2 + 3x_1 x_2 + 4 x_2^2\). Calculate \(g(2, -1)\).
Hint
This is the same functional expression as in the previous question, so method and answer are the same.
Question c#
Let \(\alpha \in \mathbb{R}\). Find \(g(2 \alpha, \alpha)\) and \(g(\alpha, 2 \alpha)\), where \(g\) is defined in the previous question. Calculate the derivative of \(g(2 \alpha, \alpha)\) with respect to \(\alpha\).
Hint
For \(g(2 \alpha, \alpha)\), substitute \(x_1 = 2 \alpha\) and \(x_2 = \alpha\) into \(g(x_1, x_2) = x_1^2 + 3x_1x_2 + 4x_2^2\). Repeat for \(g(\alpha, 2 \alpha)\). For the derivative, differentiate the expression for \(g(2 \alpha, \alpha)\) with respect to \(\alpha\).
Answer
Substituting gives:
\(g(2 \alpha, \alpha) = (2\alpha)^2 + 3(2 \alpha)(\alpha) + 4(\alpha)^2 = (4+6+4)\alpha^2 = 14 \alpha^2\) and \(g(\alpha, 2\alpha) = (\alpha)^2 + 3(\alpha)(2\alpha) + 4(2\alpha)^2 = (1+6+16) \alpha^2 = 23 \alpha^2\).
The derivative of \(g(2 \alpha, \alpha) = 14 \alpha^2\) with respect to \(\alpha\) is \(\frac{d}{d\alpha} \big( 14 \alpha^2 \big) = 28 \alpha\).
II: Level Curves#
Describe the level curves (contour lines) for the function \(f: \mathbb{R}^2 \to \mathbb{R}\) given by \(f(x, y) = x^2 + y^2 - 5\).
Hint
For example, use Python. The level curve for \(f(x, y) = 9\) can be plotted as follows:
x, y = symbols("x y", real=True)
f = x**2 + y**2 - 5
dtuplot.plot_implicit(Eq(f,9), (x,-10,10), (y,-10,10))
III: Graph or Level Curve?#
Below are shown the graph of a function \(f_1\) of one variable and a level curve of a function \(f_2\) of two variables. Which plot is the graph, and which is the level curve?
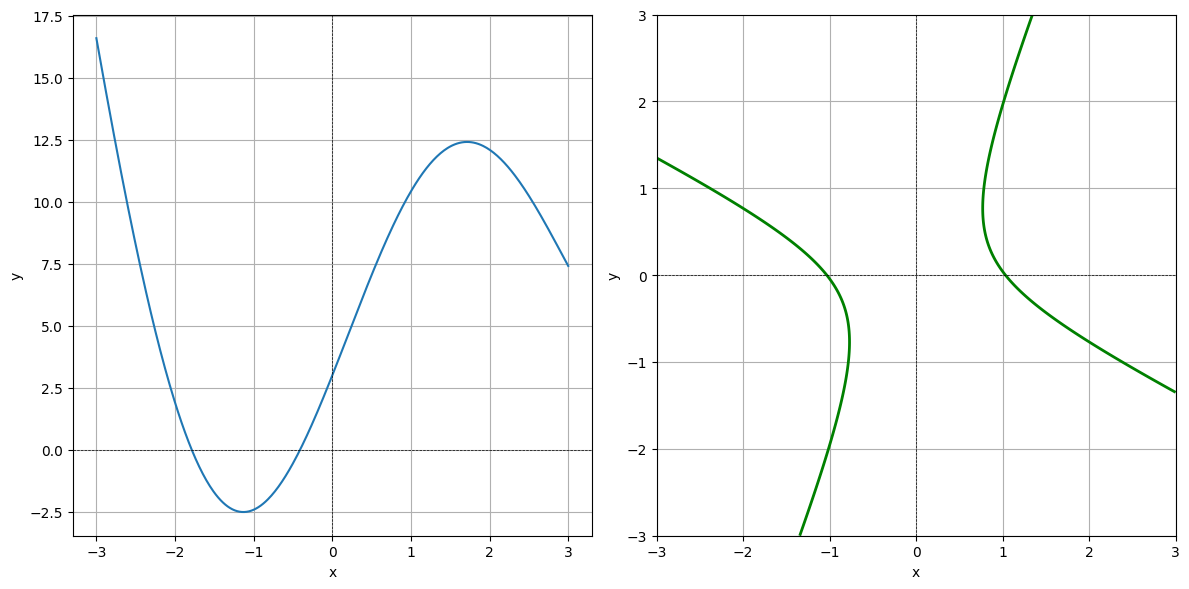
IV: Discontinuous at One Point#
Draw, describe, or define a function \(h: \mathbb{R} \to \mathbb{R}\) that is continuous at all points except for a single point.
Answer
One possible function is \(h(x) = \begin{cases} x & \text{if } x \neq 1 \\ 0 & \text{if } x = 1 \end{cases}\). This function is continuous everywhere except at \(x = 1\).

